Price Elasticity—the Good, the Bad, and the Ugly

Price is the most important profit lever. Increasing prices without a loss in demand is more profitable than increasing units or decreasing variable or fixed costs.

Unfortunately, demand reacts to price changes, and a price increase generally leads to a decrease in demand.

Therefore, it is crucial to measure how customers react to price changes. This is done using the price elasticity of demand—in short, price elasticity.

In this and our follow-up articles, we take a closer look at key facets of price elasticity: 

The Good: How, in simple cases, price elasticity can be used to maximize revenue or profit. 
The Bad: How, in most cases, price elasticity cannot be estimated with the necessary precision to be useful for pricing. 
The Ugly: How, in a market with multiple products and competition, pricing on price elasticity completely falls apart.

What is Price Elasticity?

Price elasticity describes the relationship between price and demand. It is defined as the ratio between the percentage change in demand and the percentage change in price*. For example, if the price increases by 1% and demand decreases by 2%, the price elasticity is -2% / 1% = -2.

Let’s see if we can illustrate these equations using a simple example. Assume we operate a lemonade stand and want to find the ideal price. We offer only one product—a cup of lemonade—and are the only supplier in town.

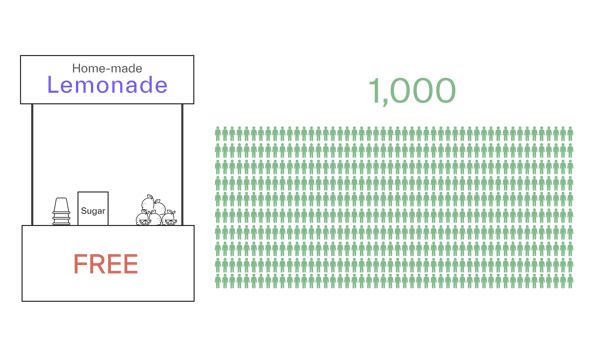
We charge $0.50 per cup (for lemons, sugar, ice, water, and the cup), and from a “Free Trial,” we know the market size is 1,000 cups per day.

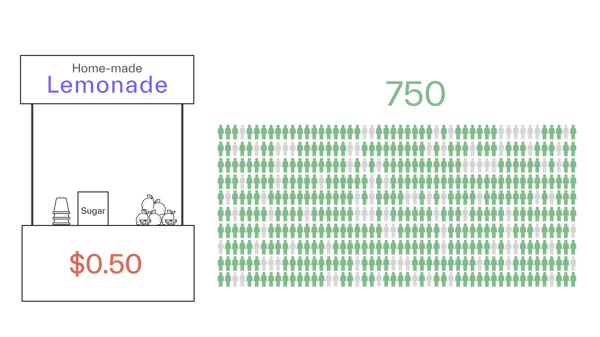
If we charge $0.50 per cup (i.e., zero margin), we sell 750 cups. This means that 250 people have a willingness to pay less than $0.50.

We make a revenue of 750 x $0.50 = $375 and a profit of 750 x ($0.50 – $0.50) = $0.

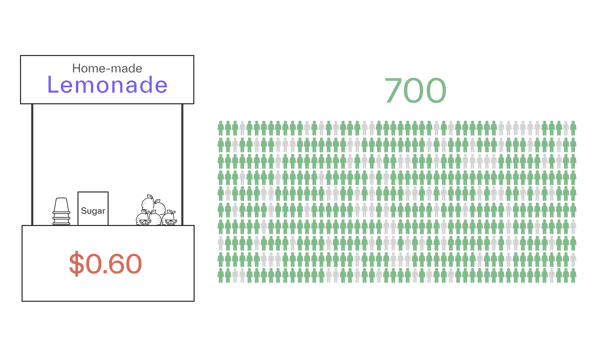
If we increase the price to $0.60 (+20%), we might lose another 50 people, all of whom have a willingness to pay between $0.50 and $0.60, and sell 700 cups (-6.7%).

Therefore, the price elasticity for this price range is -6.7% / 20% = -0.33. Our revenue is 700 x $0.60 = $420, and our profit is 700 x ($0.60 - $0.50) = $70.

If we continue this experiment by changing the price in steps of 5 cents until no one buys from us anymore, we get the relationship between price and demand shown in Graph A.

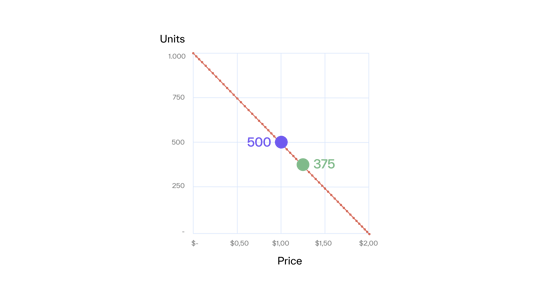
Graph A

Our price demand function is linear, i.e., we lose the same absolute number of units for every 5 cents we increase. In this example, demand is determined only by our price. In realistic situations, demand is influenced by more factors. The most important are:

• Seasonality, events (the weather, holidays, etc.), and chance (e.g., if individual people feel like having lemonade today). We will look at the influence of these circumstances in the next blog.
  
  
• Alternative options that we offer (e.g. if we also offer grapefruit juice at a certain price) and that the competition offers (e.g., a lemonade stand across the street). We will look at this in blog 3 of this series.

We can derive price elasticities using the price elasticity formula (Graph B). Elasticity is not constant but increases with price.

This is an important point: Price elasticity generally changes with price**. Therefore, no one number characterizes the relationship between price and demand.

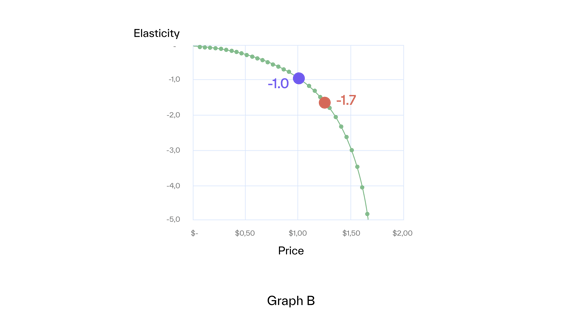
Inelastic price range

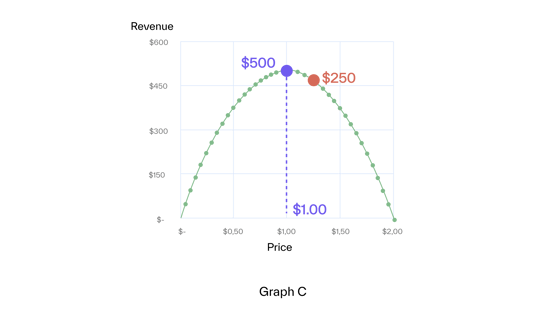
The price range with an (absolute) elasticity of less than one (in our example, from $0.00 to $1.00) is called inelastic. In the inelastic range, we gain revenue by increasing price (Graph C) since the percentage decrease in demand is smaller than the percentage increase in price.

The maximum revenue is reached at the limit of the inelastic range, at elasticity -1, where marginal units loss equals marginal price increase. This rule applies in general.

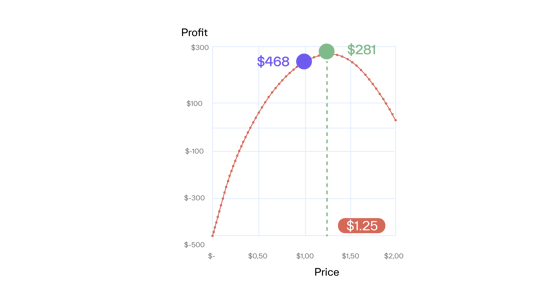
Because profit is always smaller than revenue (for non-zero costs), profit also increases (Graph D). Therefore, price increases are a good idea in the inelastic range regardless of whether you care for revenue or profit.

Elastic price range

The price range with an (absolute) elasticity of more than one (in our example above $1.00) is called elastic. Here, the percentage decrease in volume is larger than the percentage increase in price, i.e., we lose revenue when we increase price.

However, profit keeps increasing with price until the Margin x the Elasticity = -1. In our example, this is the case for $1.25 (Graph D).

From that formula, we see that the lower the margin, the higher the elasticity at the profit optimum and, consequently, the larger the difference between the revenue and profit optimal price.

For example, if there was a bad harvest, lemon prices might explode, and our costs would double to $1.00 per cup. We would need to move further into the elastic range of $1.50 to optimize our profit.

Here, the margin is 33%, and the elasticity is -3. We passed half of our cost increase (+$0.50) on to customers as a price increase (+$0.25).

This is a general rule for linear demand functions: If costs change, half of the change should be passed on to customers to maintain the profit optimum. For other demand functions, costs are passed on differently.

For example, in the multiplicative demand function, the percentage price change must be equal to the percentage cost change—i.e., in the example above with a cost increase of 100%, the price increase would also have to be +100%, which leads to a new price of $2.00 vs. the $1.50 under a linear demand function.

Pricing is very sensitive when understanding demand!

The "Good" In Price Elasticity

The Good about price elasticity is that we can use it to determine the optimal prices for revenue and profit***:

• In the revenue optimum: Elasticity = -1

• In the profit optimum: Elasticity * Margin = -1

In the next article, we will investigate the Bad (measurement) and the Ugly (multiple products and competition) of price elasticity.

Get Started Today to Reach Your Goals Tomorrow 

Request a demo today to see how Buynomics supports your RGM team and helps you make data-driven decisions across all RGM levers, including pricing.